Дослідження оптимізації параметрів в алгоритмах машинного навчання для дискримінації опорно -рухового завдання за допомогою носячих датчиків

Учасники

Учасники (П. = 35, 19 ♂10 ♀, 27,4 ± 26,5 років, 1,74 ± 0,8 м, 71,5 ± 11,3 кг) без відомих травм або хвороб на момент тестування. Учасники підписали письмові форми поінформованої згоди до участі. Дослідження проводилось відповідно до Декларації Гельсінкі та затверджено Інституційним комітетом з етики людини університету Ноттінгем Трент (Кодекс протоколу 595 28 жовтня 2020).

Експериментальний дизайн

Учасники приїхали до університету, одягаючи футболки, шорти або гернінси на шкірі та власні тренери. Вони виконали три завдання руху на 12-метрову доріжку (рис. 2). Кожна умова вимагала від учасників ходити або по самостійному повільному, нормальному або швидкому темпі; Відповідно до вказівок, наданих усім учасникам, “нормальний” повинен був бути швидшим, ніж “повільний” стан, і “швидкий” повинен був бути швидшим, ніж звичайний стан. Середня швидкість ходьби для повільних, нормальних та швидких умов становила 0,8 м/с (± 0,22), 1,1 м/с (± 0,07) та 1,3 м/с (± 0,10) відповідно. Учасники пройшли загалом 120 м для кожної з трьох умов ходьби, а порядок експериментальних умов був рандомізований між учасниками за допомогою генератора випадкових чисел та періодів однохвилинних тихих умов.

ІнструментаріяБули використані трисні датчики акселерометра (Axivity Ax6, Йорк, Великобританія), відібрані при 100 Гц та 8 г діапазону. Датчики були прикріплені до шкіри двосторонньою клейкою стрічкою на крижах, приблизною серединою бічної лівої та правої стегна сегментів та приблизної середини бічних лівих і правих хвостовиків (рис. 2). Датчики були налаштовані для запису прискорень у ортогональних площинах X, Y та Z. Всі сигнали акселерометра були візуально перевіряли та залишалися в межах ± 8 г, як очікувалося для ходьби.

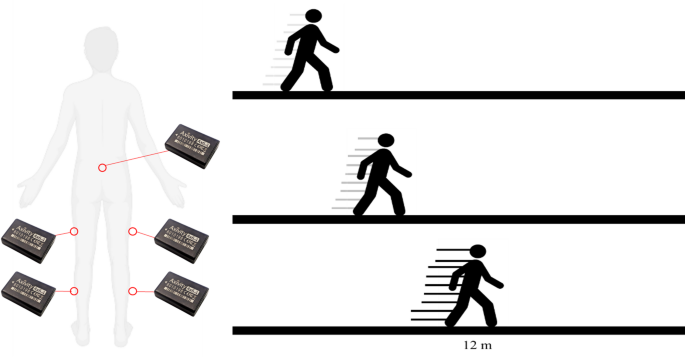
П'ять датчиків Ax6 Ax6 були прикріплені до крижів, середини бічних стегон та середньої точки бічних сегментів хвостовки. Учасники завершили три експериментальні умови: повільна, нормальна та швидка ходьба. Загальна відстань 120 м була завершена за умовою на доріжці 12 м.

Попередня обробка

Був використаний масштабність вектора прискорення для сирого часу прискорення: \ (a = \ sqrt {{a} _ {x \:}^{2}+{a} _ {y \:}^{2}+{a} _ {z}^{2}} \)

Лінійна інтерполяція дозволила синхронізацію кожного акселерометра до однієї цифрової марки часу, оскільки було виявлено, що датчики мають незначні зміни частоти вибірки, хоча вони були попередньо встановлені до 100 Гц.

Алгоритм базової машини

До вивчення будь -якої оптимізації був виконаний базовий алгоритм, що складається з початкових параметрів, із значеннями параметрів, вибраними з попередніх робіт¹⁸. Двовимірний аналіз трансформації Фур'є (2DFT)²³ було реалізовано як особливість для аналізу сигналу прискорення сировини для кожної експериментальної умови (рис. 3). Для навчання машинного навчання особливості сигналу з довжиною вікон три секунди були обрані з періодів відомої категорії ходи (повільно, нормально або швидко). Тимчасова роздільна здатність, що визначає тривалість часу даних, що використовуються для обчислення одного частотного спектру, встановлювали на 300 мс. Коефіцієнт перекриття вікна в 50% застосовувався для сегментації даних про часової області для посилення виявлення характеристик перехідної частоти під час аналізу 2DFT. Це призвело до того, що сусідні сегменти поділили 50% їхніх точок даних.

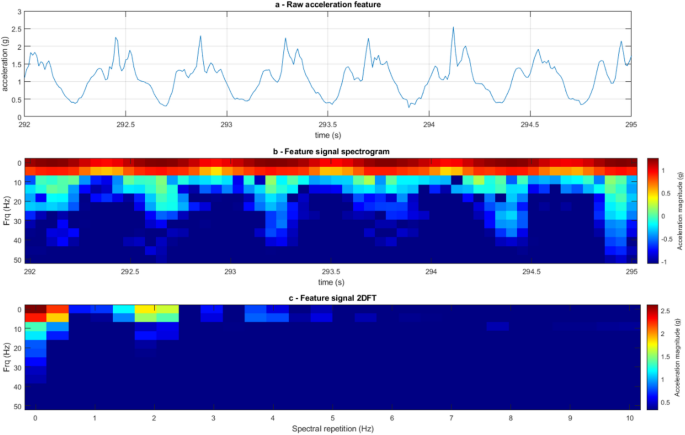
() Часовий перебіг сигналу прискорення сирого прискорення під час звичайної ходьби, демонструючи шість піків амплітуди прискорення протягом трьох секунд. (б) Спектрограма трисекундного сигналу прискорення підкреслює шість періодів великої пропускної здатності. (c) Двовимірне зображення перетворення Фур'є експериментального стану підкреслює спектр повторного сигналу, трохи нижче двічі в секунду.

2DFT застосовували індивідуально до кожного вибраного трисекундного тривалого вікна, генеруючи функції виключно у представленні частотного домену, як описано в попередній роботі¹⁸. Цей підхід гарантував, що отримана функція залишається послідовною незалежно від абсолютних термінів або фази конкретного вікна аналізу. Потім матрицю 2DFT розтягували у формат масиву. Кожен масив 2DFT потім був укладений, створюючи нову, більшу матрицю 2DFT з десятьма розтягнутими функціями для кожної умови ходьби (рис. 4). Ці матриці візуально розкрили групи з аналогічною фундаментальною частотою та пов'язаними з ними гармоніками, присутніми в сигналі прискорення для заданої категорії ходи, що дозволяє спостерігати за повторними спектральними моделями. Серія 2DFT була ретельна за допомогою візуального огляду, що було вирішальним для ідентифікації та виключення будь-яких випадків помилки, зокрема, коли ненавмисно вибирають сегменти даних, що містять сигнали, в яких учасники оберталися навколо конусів на доріжці або періодів прискорення ходи або уповільнення.

Згодом також була розрахована матриця більш високої щільності 2-мірних функцій перетворення Фур'є. Спираючись на початкову десятку функцій на категорію ходи, використовуючи 2DFT з кроком часу 0,1 с, що триває тривалість однієї секунди, було обчислено нову навчальну базу даних (TDB). Це сканування високої щільності дало 100 особливостей для кожного експериментального стану. Це призвело до загальної кількості 300 спектрів 2DFT. Обчислення як високої, так і низької щільності TDB служить окремим призначенням. По-перше, сканування низької щільності забезпечує всебічний огляд вмісту частоти в межах даних, що дозволяє проводити навчання комп'ютерних алгоритмів для дискримінації різних ходи. По-друге, додаткова матриця високої щільності є цінним інструментом для кількісного визначення ступеня відхилень, виявлених ознаками в певній умовах ходи. Мета бази даних високої щільності полягала в тому, щоб ідентифікувати компоненти, які відображали зміни та дозволяють їх кластеризацію (рис. 4).

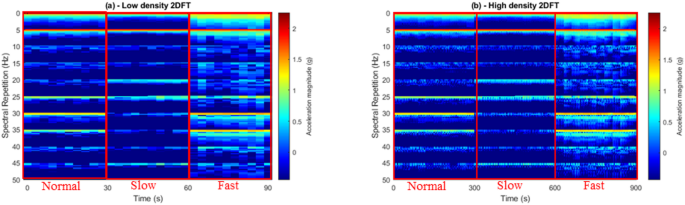
Два набори двовимірних зображень перетворення Фур'є, кожен з яких ілюструє три експериментальні умови, пов'язані з ходьбою. () Складена серія розтягнутих зображень демонструє нормальні, повільні та швидкі умови ходьби. Для кожної умови укладено десять 3-секундних спектрів, з темно-червоним і темно-синім, відповідно, що вказує на більш високі та нижчі величини прискорення (б) Серія більш високої щільності фіксує однакові експериментальні умови, але при температурі сканування на 0,1 с протягом однієї секунди, в результаті чого спектри 100 × 3 секунди на стан. Прямокутні вибори підкреслюють нормальні, повільні та швидкі умови ходьби в обох наборах зображень.

Простий алгоритм машинного навчання, що складається з аналізу основних компонентів (PCA) та аналізу дискримінантних функцій (DFA), був використаний у кожній бази даних навчальних навчальних закладів, щоб забезпечити кластеризацію модальностей ходи з подальшим кількісним визначенням відхилень навколо центроїду. PCA проводили шляхом діагоналізації матриці коваріації, оскільки всі вхідні параметри складаються з даних акселерометра. Основні оцінки компонентів (набір значень, які перетворюють залежну змінну в багатоваріантній базі даних у зменшений набір основних компонентів²⁹ були створені для кожного експериментального стану. Основні компоненти для кожної змінної обчислювались до 80_то перцентиль. Цей підхід зафіксував 80% від загальної дисперсії в кожній модальності ходи, учасника та датчика, забезпечуючи пристосованість до властивої мінливості в кожному наборі даних.

Аналіз дискримінантних функцій (також відомий як лінійний дискримінантний аналіз) визначив дискримінаційні особливості між способами ходи для подальшого кластера зменшених даних про розмірність, як цього вимагає користувач. DFA – це контрольована методика навчання, яка оптимізує дискримінацію між заздалегідь визначеними умовами²⁹.

Після застосування DFA протягом двох вимірів були побудовані оцінки дискримінантної функції (DF) 1 і 2 (рис. 5). Потім був обчислений показник критерію для оцінки якості дискримінації між трьома умовами. Цей бал був отриманий із співвідношення продукту трьох відстаней між трьома кластерами до продукту трьох стандартних відхилень кожного кластера, як це було продемонстровано в нашій попередній публікації¹⁸. Сильні дискримінаційні показники позначаються одночасно виконанням значної відстані між центроїдами та низькими стандартними відхиленнями в кожній умові. Критерій дискримінації був сформульований як наступне:

Там, де DIST_1 являє собою відстань між центроїдами швидких і нормальних хмар, DIST_2 – це відстань між швидкими та повільними центроїдними хмарами, а DIST_3 – відстань нормальних та повільних кластерних центроїдів. Scatter_01, scatter_02 та scatter_03 обчислюються шляхом визначення стандартних відхилень відстаней кожної даних, що вказують на їх центр для кожної експериментальної умови (рис. 5).

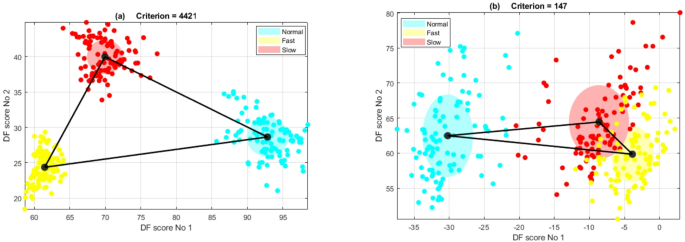
Оцінки дискримінантної функції виявляють чітку кластеризацію трьох заходів, що цікавлять. () Успішна дискримінація очевидна з оцінкою критерію, що перевищує 500. Хмарні центроїди відображають істотне розділення, а стандартні відхилення в кластерах порівняно невеликі. (б) Ілюструє невдалу дискримінацію, позначену оцінкою критерію нижче 500.

Експериментатори візуально вивчали ступінь перекриття між хмарами, що відповідають різним типам ходи, щоб суб'єктивно пов'язувати, приблизно, успіх дискримінації між трьома режимами руху до значення критерії дискримінації. Коли умови сильно перекриваються, дискримінація вважалася невдалим. Значення критеріїв дискримінації, що перевищує значення близько 500, найчастіше вказувало на нульове перекриття між хмарами для різних умов ходьби. Деякі перекриття між умовами спостерігалися, коли коефіцієнт критеріїв було нижче 500. Тому було обрано порогове значення критерію успіху 500. Цей поріг емпірично поводився і вирівнюється із спостережуваною відокремленістю кластеру в завданнях. Результати успішних та невдалих спроб дискримінації були задокументовані для всіх п’яти датчиків. Ця комплексна оцінка забезпечила кожне розташування датчика змістовним підрахунком успішних дискримінацій, досягнутої між трьома експериментальними умовами.

Процес оптимізації

Після розробки базового алгоритму машинного навчання (що включає параметри, встановлені на швидкість вибірки 100 Гц, довжину вікон 3 с, тимчасова роздільна здатність 0,3 с та значення, що перекриваються 50%, які не використовували нормалізацію), оптимальні параметри для дискримінації модальностей ходи систематично досліджували по одному. Кожен параметр мав свої значення вичерпно прокотиться по одному, зберігаючи всі інші, обмежені до початкового базового сканування.

Нормалізація

Першим кроком було побачити вплив нормалізації амплітуд сигналу акселерометра. Перш ніж застосувати будь -яке машинне навчання до матриць 2DFT, сигнал прискорення нормалізувався шляхом ділення кожного вимірювання на середнє значення сигналу у функції, тобто мінливість величини прискорення була видалена, забезпечуючи початковий набір даних про нормалізовані та нормалізовані сигнали.

Тимчасова роздільна здатність

Тимчасова роздільна здатність була першим параметром, який слід сканувати для оптимального значення, між значеннями 20 і 300 мс, при збільшенні етапів 10 мс.

Частота відбору проб

Другим параметром, який слід вивчити, була частота вибірки, між значеннями 25 і 100 Гц у кроках 5 Гц. Швидкість нижчі, ніж оригінал, були отримані під час післяобробки шляхом інтерполяції даних про необроблене акселерометра.

Довжина вікна

Наступний параметр, який був сканований, становив довжину вікна між 0,9 і 6 с значень з кроком 0,3 с.

Значення, що перекриваються

Кінцевим параметром, який слід вивчити, були значення перекриття. Були проаналізовані шість значень, що перекриваються: 0%, 50%, 66%, 75%, 80%та 88,34%.