DataSet Breakhis
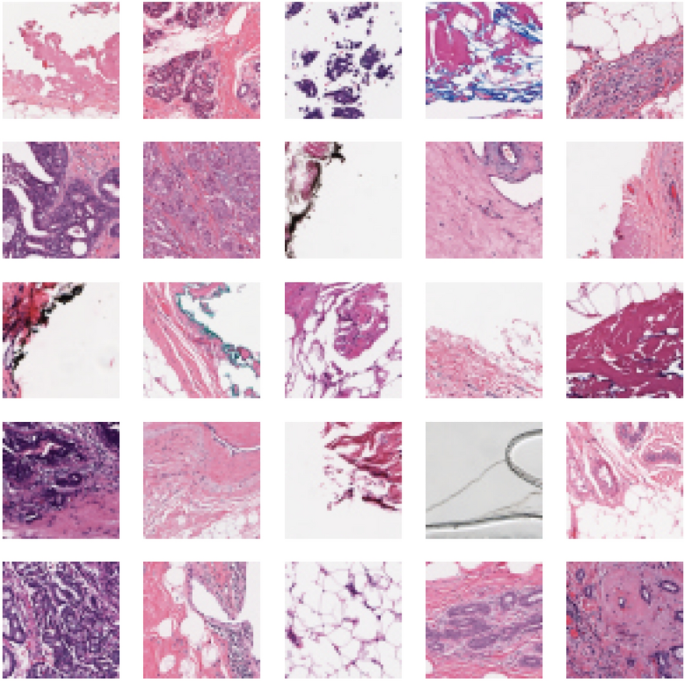
Приклади фактичних текстур, знайдені на Breakhis Images.
Гістопатологічний (BreakHis) на набір даних раку молочної залози23,24 широко використовується для досліджень та експериментів у діагностиці БК. Складаючи мікроскопічні зображення зразків тканини пухлини молочної залози, набір даних анотується різними характеристиками для полегшення розвитку алгоритмів машинного навчання та комп'ютерних систем діагностики для БК.
Основні атрибути набору даних Breakhis включають:
-
Тип зображення: Набір даних складається з гістопатологічних зображень тканин молочної тканини високої роздільної здатності, витягнутих із гістологічних слайдів.
-
Заняття: Breakhis класифікується на чіткі категорії залежно від типу пухлини молочної залози, зображеної на зображенні. Ці категорії включають доброякісні та злоякісні пухлини, додатково підрозділені на підкласи на основі типу та тяжкості пухлини.
-
Анотації: Кожне зображення в наборі даних має анотації, що містять мітки класів та підтипи. Крім того, анотації включають додаткову інформацію, таку як вік пацієнта та рівень збільшення тканин.
-
Розмір даних: У таблиці 1 представлена додаткова інформація про набір даних Breakhis та розділення даних.
У нашому дослідженні на етапі навчання було використано дві третини даних, а решта третини була виділена на фазу тестування набору даних. Малюнок 1 ілюструє збірку зображень з цієї бази даних.
Показники для оцінки
У царині завдань машинного навчання та класифікації швидкість точності тесту25 служить метрикою, що оцінює ефективність навченої моделі на незалежному наборі даних (тестовий набір), який не був частиною навчального процесу. Він кількісно визначає співвідношення правильно прогнозованих екземплярів до загальних екземплярів у тестовому наборі.
Висловлений математично, швидкість точності тесту обчислюється як:
$$ \ stage {вирівнюється} \ mathrm {{{accuracy}} = \ frac {{{{{{число}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}} {{{{total}}}}}}}}}}} {\ mathrm}}} {{число}} {\ mathrm}}}} \; \ mathrm {{прогнозування * \ quad 100 \% \ end {вирівняний} $$
(1)
Де:
-
Кількість правильних прогнозів: Кількість випадків, коли прогноз моделі відповідає фактичній справжній мітці.
-
Загальна кількість прогнозів: Загальна кількість екземплярів у тестовому наборі.
У пробігу, хоча рівень точності тесту може бути часто використовуваним показником для опитування, показує виконання, важливо розглянути встановлення інформації та проблему, щоб вирішити, чи це головна відповідна метрика для використання або у випадку, якщо інші вимірювання повинні бути використані для більш повної оцінки.
Контур запропонованого підходу
Для покращення вилучення функцій була розроблена модель глибокого навчання з неглибокою архітектурою для класифікації зображень. Це просування передбачало злиття аналізу багатороздільної здатності для вилучення функцій та Adaboost як лінійного класифікатора. Поєднання цих методик призвело до створення глибокого складеного вейвлет-авто-ендера (DSWAE) з нещодавно розробленої моделі WN, відомої як глобальна мережа вейвлет (GWN). Малюнок 2 ілюструє запропоновану методологію класифікації 2D зображень раку молочної залози, що використовують DSWAE.
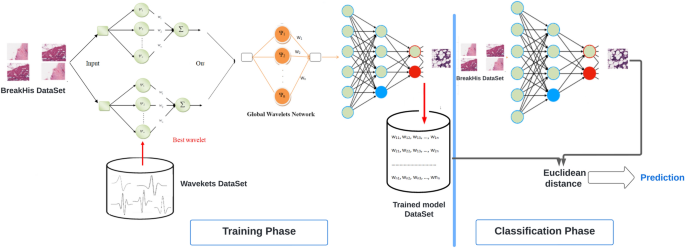
Система класифікації для 2D BC -зображень на основі DSWAE.
Як зображено на фіг. 2, запропонована система складається з двох основних компонентів: фази навчання та етапу класифікації. Під час фази тренувань наша мета – розробити DSWAE, використовуючи SWAE для представлення 2D -зображень раку молочної залози. Апсевдокод для всього процесу нашої системи представлений в алгоритмі 1.

Створення системи DSWAE.
Розробка SWAE
Спочатку ми генеруємо WN для кожного класу зображень, присутнього в навчальному наборі даних. Конструкція цих WNS використовує найкращий алгоритм внеску26,27окреслений на фіг. 3. Під час цієї фази одновимірний WN побудований за допомогою швидкого вейвлет-перетворення (FWT)28,29,30,31. Для оцінки ефективності нашого підходу до моделювання зображень використовується пікове співвідношення сигнал-шум (PSNR).
Далі ми використовуємо вейвлетські бали, щоб зробити GWN. GWN збирається моделювати зображення, що відображає один клас із бази даних, відомої як C1. Ми показуємо результати у двох таблицях32. Перший набір включає WNS зображень, що належать до категорії С1, як зображено в таблиці 2. Другий набір містить WNS решти зображень у наборі даних, позначених як C2.
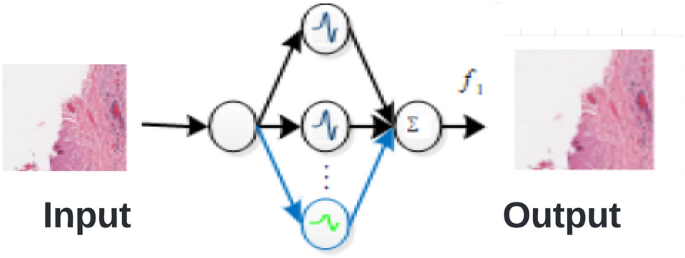
Далі ми обчислюємо загальну кількість всіх вейвлетів, що використовуються в С1, з урахуванням кожного вейвлета та його позиції. Згодом глобальна мережа вейвлет (GWN) побудована шляхом вибору найвидатніших вейвлетів на основі їх частоти виникнення. Оптимальний вейвлет для кожної позиції визначається його найвищим значенням балів, як показано в таблиці. 3.
Після обчислення балів вейвлет (таблиця (4)) створюється новий GWN одного класу.

Формування GWN з використанням найкращих балів вейвлетів.
На рис. 4 ми використовували найкращі коефіцієнти, щоб знайти вейвлети, які складають GWN. На цьому кроці кожен клас даних показаний GWN. PSNR використовується для вимірювання того, наскільки добре працює кожна мережа.
Здійснюючи GWN для кожного класу в наборі даних, ми перетворюємо їх усі в WAE. На малюнку 5 показано, як зробити WAE з GWN32.
Моделювання класу за допомогою WAE.
Отже, декодоване зображення, що утворюється з WAE, обчислюється наступним чином:
$$ \ stage {вирівнюється} \ лівий \ {\ stage {array} {l} \ лівий \ langle {{\ psi _i}, {{\ tilde {\ psi} _ j}} \ right \ rangle = 0 \ quad \ quad i \ ne j \ else \ rangle \ qually, якщо \ quad i \ ne j \ else \ reably \ qualblean {{\ psi _i}, {{\ tilde {\ psi}} _ j}} \ right \ rangle = 1 \\ \ end {array} \ right. \ end {вирівняний} $$
(2)
Більше того, нейрони в прихованому шарі WAE використовують лінійну функцію, яка може бути виражена рівнянням. (3):
$$ \ stage {aligned} \ start {array} {*{20} {l}} {f = {x_1}, {x_2}, {x_3}, … {x_n}} \\ {{\ hat {f}} = {{{\ hat {x}}} _ 1}, {{{\ hat {x}}} _ 2}, {{{\ hat {x}}} _ 3}, … {{\ hat {x}}} _ n}} \ {\ \}} _ n}} \ \ \ \ \ ps = ps = ps = ps = ps = ps = ps = ps = ps = ps = ps = ps = ps = ps = pns = = ps = pns = = ps = pns = = pns = = pnsal {w_ {1i}}, {w_ {2i}}, {w_ {3i}}, … {w_ {ni}}} \\ {{{\ tilde {\ psi}} _ i} = {{{\ tilde {w}}} _ {1i}}, {{{\ tilde {w}}} _ {2i}}, {{{\ tilde {w}}} _ {3i}}, … {{{\ tilde {w}}} _ {ni}}} \ end {array} \ end {вирівняний} $$
(3)
Ми робимо рівняння (4):
$$ \ stage {вирівнюється} {a_i} = \ prec f, {\ psi _i} \ suck \ quad \ rightarrow \ quad {a_i} = \ sum \ межі _ {j = 1}^n {{w_ {ji}}} {x_j} \ кінцеві {aligned} $ $ $ $ $ $ $ $ $ $
(4)
Отже, отриманий вихід зображення SWAE отримується за допомогою рівняння. (5):
$$ \ stage {aligned} {{\ hat {x}} _ i} = \ sum \ обмеження _ {j = 1}^n {{{{\ tilde {w}}} _ {ji}}} {a_j} \ end {aligned} $$} $$
(5)
Останніми роками методики SC здобули видатність для вилучення функцій з різними алгоритмами, які намагаються зняти рідкісні зображення зображень за допомогою методів оптимізації. SC також знайшов інтеграцію в глибокі нейронні мережі, використовуючи непідконтрольні алгоритми навчання, щоб забезпечити обмеження розрідження на прихованих одиницях. Основна ідея розрідженого кодування – це рідкість. Простіше кажучи, ми говоримо, що сигнал рідкий, коли ми можемо описати зображення, використовуючи лише кілька основних частин, про які ми вже знаємо. Щоб подумати більш критично, ми можемо зробити зображення, яке ми намагаємося запам'ятати менш детально, використовуючи розріджене кодування, яке використовується в мозку33. Парсимонічне кодування відноситься до принципу мінімізації кількості нейронів, активованих для представлення інформації. Це ефективне використання нейронних ресурсів підвищує здатність мережі розмежувати елементи в її пам'яті, що дозволяє включити додаткові вивчені повідомлення. По суті, Parsimony сприяє різноманітності шляхом оптимізації розподілу ресурсів. У контексті обробки зображень Парсинія означає, що зображення добре виглядає з якомога менше коригувань. Ці фактори, перелічені у словнику, дозволяють показати зображення як поєднання різних речей. Цей метод робить файл зображення меншим, зберігаючи важливі деталі, тому він добре працює34. Деякі нейронні мережі, як парсимонічний АЕ35Складіть списки важливих функцій, необхідних для зберігання інформації коротко. Після налаштування мережі до вектора кодування додається розріджена частина, щоб зробити її більш рідкісною. У літературі існує багато різних способів досягти цієї мети. У нашій архітектурі ми використовуємо K-SPARSE AE36 Тому що вони прості у використанні та працюють добре. K-Sparse AE знаходить найбільшу активацію K у векторі кодування та змінює інші активації на нуль. У нашому методі ми створюємо SWAE з WAE. Матриця ваги виготовляється з використанням вейвлетів з WAE та його коефіцієнтів.
Формування DSWAE
На малюнку 6 зображено процес складання DSWAE з двома прихованими шарами. Цей архітектурний дизайн випливає з серії складених SWAE.
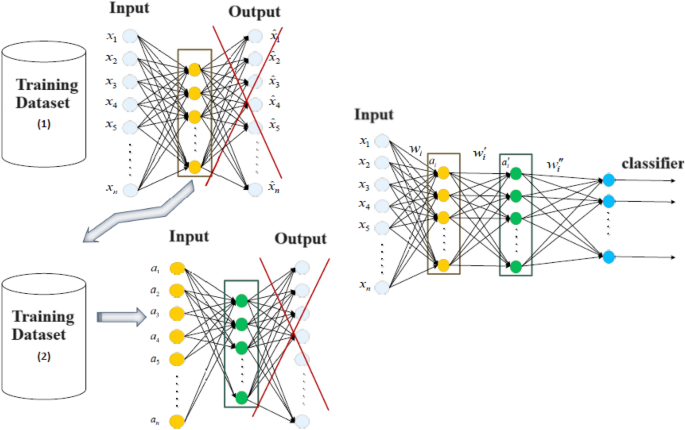
DSWAE з двома прихованими шарами.
Етап класифікації
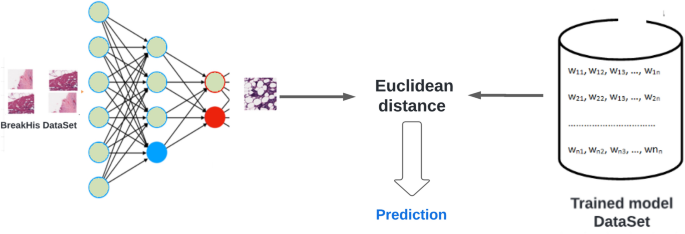
Конфігурація фази класифікації дуже нагадує фазу навчання. Фіг.7 ілюструє послідовність процесу класифікації.

Процес класифікації починається з зйомки 2D -зображень та вкладання їх у DSWAE, які були створені під час навчання. У процесі класифікації евклідове відстань використовується для пошуку подібності між зображеннями DSWAE.
$$ \ почати {вирівняний} dist = \ ліворуч \ | {a_ {i = 1}^n {v_i} {y_i} – a_ {j = 1}^n {w_j} {y_j}} \ права \ | \ end {вирівняний} $$
(6)
де \ ({{V_i} y} \) і \ ({{W_j} {y_j}} \) – це дві мережі. Евклідове відстань між двома мережами, які використовують однакові функції вейвлет, можна обчислити за допомогою цього рівняння:
$$ \ start {вирівняний} dist = \ ліворуч ({dist '\ ліворуч ({{y_ {i, j}}} \ праворуч) {dist^ {1/2}}} \ право) \ ent {вирівнюється} $$
(7)
де \ (Dist = {dist_1} …. dist_n^i \) і \ ({Y_ {i, j}} = \ ліворуч \ langle {{y_i}, {y_j}} \ right \ rangle \). Отже, порівняння двох мереж з однаковими функціями вейвлетів передбачає оцінку подібності їхніх матриць ваги.

